Tema 23: ANÁLISIS ROC

Este vídeo «La curva ROC como función matemática» comenta las siguientes tablas:

La curva ROC como función matemática

Nota: Al final del vídeo anterior comento que hay un error en la tabla con las desigualdades que se comentan. En el texto se ha corregido.

1. El Análisis ROC (Receiver operating characteristics) es una metodología desarrollada para analizar un sistema de decisión.

2. Tradicionalmente se ha usado en ámbitos de detección de señales y, en las últimas décadas, se ha utilizado mucho en Medicina.

3. En Medicina el Análisis ROC permite evaluar la calidad de un procedimiento diagnóstico. Podríamos decir que el Análisis ROC se ha transformado actualmente, en Medicina, en una tecnología para evaluar y analizar las peculiaridades de un sistema diagnóstico.

4. El Análisis ROC trabaja con las nociones de Sensibilidad y Especificidad. En el apartado dedicado a Estadística y Medicina he escrito un artículo titulado “Sensibilidad, Especificidad, Valor predictivo positivo y Valor predictivo negativo”. Sería interesante revisar allí estos cuatro conceptos. Sin embargo, como el Análisis ROC básicamente trabaja con los dos primeros: la Sensibilidad y la Especificidad, voy a revisar ahora, únicamente, las definiciones de estos dos conceptos.

5. Veamos el siguiente gráfico ya comentado en el artículo citado:

6. Puede observarse que cada rectángulo separa dos grupos: uno de personas con la enfermedad (E) diagnosticada y otro sin ella (NE). Al mismo tiempo con todos ellos se ensaya una prueba diagnóstica. Los que dan positivo (P) en esta prueba son los del cuadro interior coloreado. Y llamaremos N a los que han dado negativo en la prueba diagnóstica que son todos los que no caen dentro del rectángulo coloreado.

7. La Sensibilidad es el cociente: P/E; o sea, la proporción de positivos que tenemos entre los que tienen la enfermedad. En el dibujo anterior es la proporción que ocupa el grupo de los positivos en el interior del grupo de los que tienen la enfermedad.

8. Como puede verse en los cuatro rectángulos del dibujo, según el método diagnóstico podemos tener sensibilidades muy distintas. Evidentemente interesa un método diagnóstico con alta sensibilidad, que la mayor parte de enfermos con esa patología den positivo para la prueba diagnóstica.

9. La Especificidad mide la proporción de negativos que hay en el grupo de los que no padecen la enfermedad que estudiamos. La Especificidad será, pues, el cociente: N/NE. La Especificidad también interesa que sea alta. Interesa que quien no esté enfermo nos dé negativo en la prueba, evidentemente.

10. Si volvemos a mirar el dibujo anterior podremos ver distintos posibles métodos diagnósticos y su calidad. Como se puede ver acompañando a la flecha que indica alto o bajo se ponen unos valores porcentuales que son aproximados: 5% ó 95%.

11. En el dibujo puede observarse que el primer método diagnóstico (el de la izquierda) nos marca la situación ideal: alta sensibilidad y alta especificidad. Observemos que casi todos los positivos están en E. Y observemos también que casi todos los de E, los que tienen la patología, dan positivo. Los de E que dan negativo son los llamados falsos negativos. Los de NE positivos son denominados falsos positivos. Los falsos negativos son el complementario, el contrapunto, de la sensibilidad. Los falsos positivos lo son de la especificidad.

12. El segundo método diagnóstico esquematizado es un ejemplo de mala técnica diagnóstica. Da positivo cuando no hay enfermedad y da negativo cuando hay enfermedad. En este caso tenemos baja tanto la sensibilidad como la especificidad. Casi todos son falsos positivos o falsos negativos.

13. Tampoco es bueno lo que sucede en el tercer caso. Aquí casi siempre da positiva la técnica, haya o no enfermedad. En este caso la sensibilidad es alta pero la especificidad muy baja. Esto tampoco es bueno para una técnica diagnóstica.

14. En el cuarto caso la técnica casi nunca da positiva. Tenemos baja sensibilidad, aunque, eso sí, alta especificidad. Tampoco es buena esta situación.

 

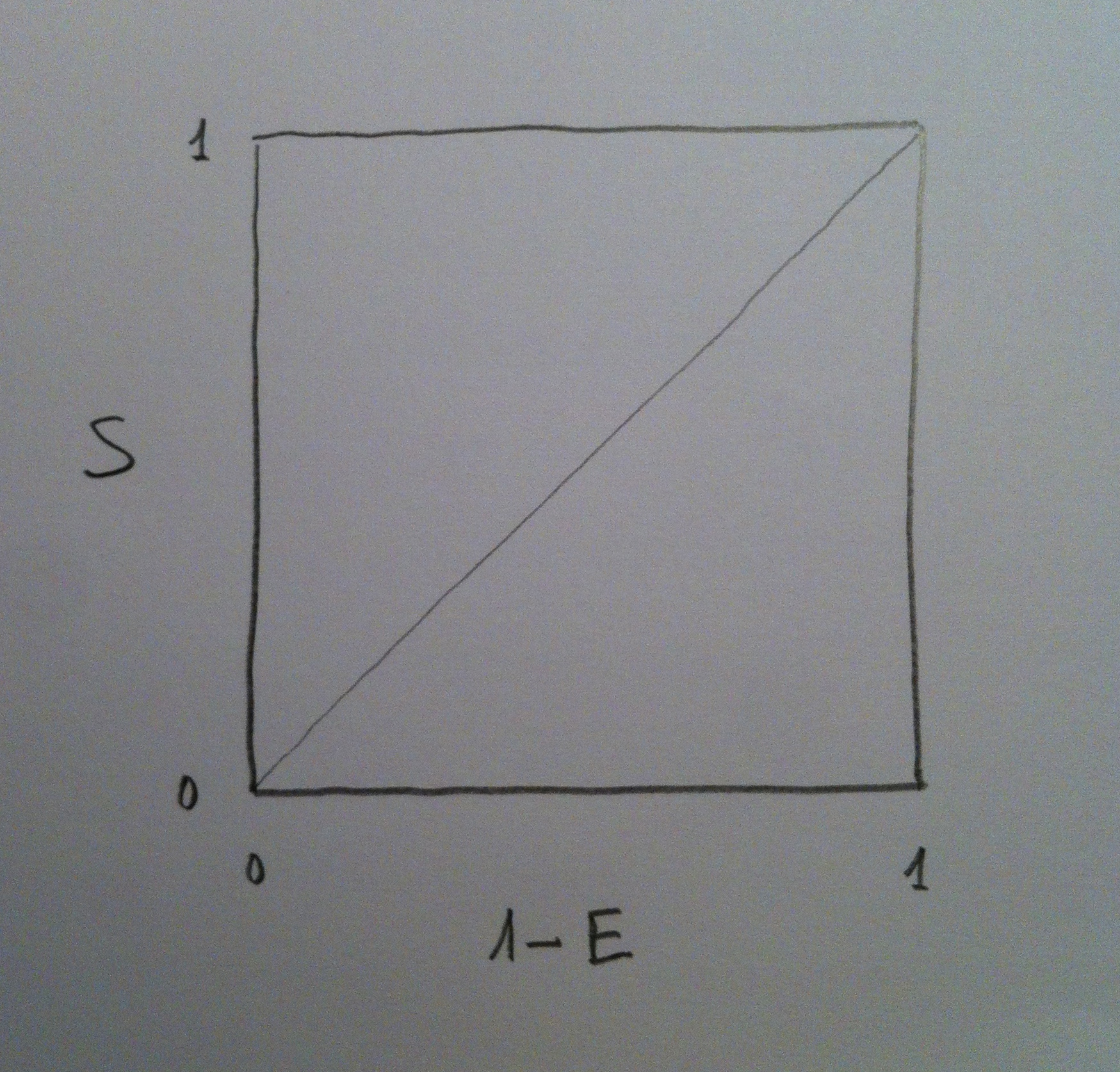
15. En el Análisis ROC suele manejarse un espacio que viene dado por la Sensibilidad (S) y 1-Especificidad (1-E). Tradicionalmente se trabaja con este valor: 1-E y voy a seguir aquí, evidentemente, esta tradición. Este espacio es muy importante. Veámoslo bien. Veamos el gráfico siguiente:

16. En el eje de las abscisas se sitúa, como puede verse, el valor de 1-E y en el eje de las ordenadas se sitúa el valor de S.

17. Es muy interesante darse cuenta de las zonas de este gráfico. Suele dibujarse una diagonal: la que va del punto (0, 0) al punto (1, 1).

18. Observemos en el siguiente gráfico unos cuantos puntos y veamos, también, la combinación de Sensibilidad y de Especificidad que cada uno de ellos representa:

19. Observemos que la situación ideal es estar cerca del punto (0, 1); o sea, del vértice superior izquierdo, que es donde hay, al mismo tiempo, mucha Sensibilidad y mucha Especificidad. Y observemos, también, que el triángulo inferior indica un método diagnóstico desastroso: sería peor que tomar las decisiones al azar.

20. El gráfico siguiente es también una representación de diferentes puntos en el espacio ROC pero haciendo ahora, para cada punto, una representación mediante un dibujo como el presentado al explicar las nociones de sensibilidad y especificidad:

21. Ante un método diagnóstico suele darse un valor de Sensibilidad y de Especificidad. Es muy habitual leer en un libro de Medicina, en la parte dedicada a métodos diagnósticos de una determinada patología, que una prueba diagnóstica concreta tiene, por ejemplo, una sensibilidad del 98% y una especificidad del 75%, y cosas como esta.

22. Este tipo de información puntual nos daría un punto en el espacio diseñado en el Análisis ROC que hemos dibujado antes. Y es una información interesante y muy útil para valorar una prueba diagnóstica y para compararla con otras que tratan también de diagnosticar una determinada enfermedad.

23. Pero el Análisis ROC va más allá de dar un único punto. El objetivo básico del Análisis ROC es dibujar una curva. Dibujar la llamada curva ROC e incluso calcular un área bajo dicha curva: la llamada AUC (Area under curve). Que es un valor que va de 0 a 1, como veremos luego.

24. La curva ROC de una situación diagnóstica determinada consiste en dibujar los distintos pares de valores de S y de 1-E que tendríamos si fuéramos cambiando el criterio de decisión. De esta forma, se analiza, para todos los posibles criterios de decisión, de un método diagnóstico, cuáles son los valores de S y de 1-E. Esto es lo interesante, pues, de este análisis: que dibuja el mapa de todos los resultados que podríamos tener ante todos los posibles criterios de decisión en una técnica diagnóstica concreta. Esto es, realmente, un muy interesante análisis de un procedimiento diagnóstico.

25. Pensemos que en la mayor parte de pruebas diagnósticas al final se trata de decidir dentro de un más o menos amplio número de situaciones posibles cuáles de ellas nos llevan a decir que tenemos enfermedad o que no la tenemos: que es diabético o que no lo es, que tiene la tuberculosis o que no la tiene, etc.

26. Suele denominarse «cutoff» al umbral de decisión para decantarse por una afirmación u otra. Es cambiando el cutoff, cambiando el criterio de decisión, como podemos ir calculando la curva ROC. En la medida que vayamos cambiando el criterio de decisión iremos obteniendo distintos pares de valores (S, 1-E). Al final, juntando estos valores, obtendremos una curva: la curva ROC.

27. Para dibujar la curva ROC buscamos unos valores reales, una muestra, unas personas de las que tengamos toda la información: debemos saber, en nuestro caso, la altura y el sexo de cada una de ellas. En el caso de estar trabajando en el diagnóstico de una patología hemos de partir de una serie de personas con y sin la patología a estudiar y a las que les aplicamos, a todas, el método diagnóstico.

28. Esto de partir de valores reales, de una muestra, para poder establecer un procedimiento, es algo que está siempre presente en Estadística. Lo hemos visto, por ejemplo, en todas las técnicas de Regresión. Necesitamos siempre una muestra para poder evaluar con ella la calidad de un procedimiento, para evaluar y estimar cómo irán las cosas cuando nos enfrentemos al reto de tener que diagnosticar.

29. Por lo tanto, en la valoración de la calidad de un método diagnóstico hacemos lo mismo, pues, que hacemos en la Regresión: tomar una muestra de valores donde lo tengamos todo y así podamos hacer una valoración de la calidad de un método diagnóstico. Es como hacer un trabajo de laboratorio previo a enfrentarse con la realidad, como ensayar algo en una planta piloto, como hacer pruebas a un nuevo coche antes de salir al mercado.

30. Veamos un ejemplo. Supongamos que queremos clasificar como hombre o mujer a una determinada persona de la que sólo tenemos la altura. Queremos establecer un valor, un cutoff, un umbral, por encima del cual pronosticaremos, “diagnosticaremos”, que aquella persona es un hombre y por debajo del cual diremos que es una mujer:

 

31. Observemos que tenemos una muestra de 5 mujeres y de 5 hombres de los que tenemos su altura. Y que están solapados. Hay mujeres en la muestra más altas que algunos hombres, por lo tanto, establecer un método diagnóstico de hombre en base a una altura, a un cutoff altura, nos generará algún error, no es un procedimiento perfecto.

32. Veamos cómo lo calculamos: Observemos que vamos cambiando el cutoff, vamos a buscar todos los posibles cutoff que nos darían lugar a resultados diferentes. Es lo que vamos haciendo en el ejemplo propuesto.

33. Para cada caso se calcula la S, la E y la 1-E. Y cada pareja de valores (S, 1-E), para cada cutoff posible, se va dibujando en el gráfico ROC. Y al final se juntan los puntos en una curva: la curva ROC. Que en el gráfico aparece en azul.

34. Miremos algún caso concreto de los que se adjuntan en esta tabla de valores. Por ejemplo, el primero. Si se elige como cutoff, como punto de decisión, menor que 160 cm, entonces todos los hombres quedarán bien clasificados como hombres: tendremos una sensibilidad del 100%, o de 1, en tanto por uno. Pero el problema es que la especificidad es horrible, porque las cinco mujeres quedarían también clasificadas como hombres: Esto nos da una especificidad del 0%, por esto el punto está arriba y a la derecha, en el punto (1, 1), porque tiene un valor S=1 y un valor 1-E=1, al ser la E=0.

35. Cojamos otro caso. El segundo: Si el cutoff es un valor mayor que 160 pero menor que 163 entonces los cinco hombres seguirán estando bien clasificados, y entre las mujeres cuatro seguirán estando clasificadas como hombres. La sensibilidad es del 100% y la especificada es, ahora, del 20%. Por esto el punto ahora está en el (1, 0.8).

36. Si vamos subiendo el cutoff dentro de todos los intervalos posibles entre valores de nuestra muestra acabaremos viendo que los puntos obtenidos son los representados y que la curva ROC es la dibujada.

37. El área bajo esta curva ROC es el AUC. Al tener el cuadrado un área máxima de 1, el valor de AUC va del 0 al 1. En nuestro caso el área sería la remarcada bajo la curva ROC:

38. Cuanto más próximo a 1 sea esa área significa que es mejor método diagnóstico, evidentemente. Significa que estamos ante un método diagnóstico con más posibilidades de discernir este enfermedad y no enfermedad. Por lo tanto, veamos cómo de izquierda a derecha en el siguiente gráfico vamos perdiendo capacidad en los diferentes métodos diagnósticos:

39. Las curvas posibles son muchas. Observemos, por ejemplo, las dos siguientes, que tendrían una misma AUC pero un perfil de curva diferente:

40. Observemos que el ejemplo que he puesto de cálculo de la curva ROC es a efectos de comprensión. Pero así se ve bien cómo se calculan esas curvas en casos reales de métodos diagnósticos. Por ejemplo, supongamos el caso real del diagnóstico de diabetes en función del resultado analítico de glucosa en sangre después de 2 horas de una sobrecarga de 75 gramos de glucosa. Si ante una situación diagnóstica como esta, con una muestra de pacientes amplia, fuéramos cambiando el cutoff de la glucosa, construiríamos la curva ROC de esta importante prueba diagnóstica en diabetes mellitus. Suele darse un cutoff de 200 mg/dL para el diagnóstico. Si tuviéramos una muestra con pacientes diagnosticados de diabetes y con personas libres de esa enfermedad y les aplicáramos ese método diagnóstico y fuéramos cambiando, entonces, de valores de cutoff, obtendríamos la curva ROC de este método diagnóstico.

41. La forma de la curva tiene que ver con lo segregados que estén los enfermos y los no enfermos respecto al criterio seguido en el procedimiento diagnóstico. Veamos el siguiente gráfico que ilustra esta afirmación:

42. Observemos a la izquierda tres situaciones bien distintas, donde tenemos una medida de alguna variable, como podría ser la cantidad de alguna medida usada como criterio diagnóstico. El grupo de enfermos y el grupo de no enfermos, en el caso de arriba, están muy separados, esto irá, lógicamente, asociado a una curva ROC con AUC próxima a 1, como puede verse. En el caso del medio la separación entre ambos grupos no es tan buen y ello va asociado de una curva con menor AUC. Finalmente en el caso de abajo los grupos están muy solapados. En este caso la capacidad diagnóstica se reduce muchísimo y esto se refleja en una curva ROC muy mala, con una AUC muy baja.

43. Esto es lo interesante, pues, del Análisis ROC: poder, con estas herramientas, establecer una medida de calidad de un procedimiento diagnóstico. Tener un dibujo de su comportamiento y una medida de su calidad.

44. Veamos en la siguiente fotografía un gráfico de un artículo en una importante revista médica donde se usa el Análisis ROC para evaluar métodos de pronóstico de infarto de miocardio:

45. Hay algo importante que no he dicho hasta ahora de estas curvas ROC. Observemos que estas curvas las construimos en base a una muestra. Por lo tanto, la curva ROC que obtenemos es una estimación de la curva real, como siempre en Estadística. Que si la muestra es pequeña es posible que no sea significativa, que no sea distinta a la que podríamos obtener al azar.

46. Se pueden construir, pues, intervalos de confianza de estas curvas ROC. El AUC también puede ser o no significativo, puede construirse un intervalo de confianza también de él. Etc. Estamos, pues, ante un caso de inferencia y, por lo tanto, como tal, sometido a todas las limitaciones y procedimientos que la inferencia nos aporta y que hemos ido viendo en temas anteriores.