Toda la explicación que a continuación tenéis del Análisis de componentes principales la podéis seguir, también, paralalamente, con la explicación de los siguientes vídeos:
1. El Análisis de componentes principales (ACP) es una técnica estadística descriptiva que tiene como punto de partida una matriz de datos con una serie de individuos a los que se les ha medido varias variables. Por eso suele clasificarse como una técnica multivariante. Para guiarnos en esta técnica vamos a manejar unos datos como los que a continuación muestro:
2. Se trata de unos datos que todos comprendemos perfectamente porque todos hemos sido estudiantes. Se trata de las notas de diferentes materias que obtienen 15 alumnos de bachillerato. Tenemos, pues, 15 individuos en el estudio; o sea, una muestra de tamaño 15 pero con ocho variables, tantas como asignaturas tenemos.
3. Si quisiéramos representar los 15 alumnos de esta muestra en un gráfico lo podríamos hacer tomando dos notas y representando los 15 puntos según sus valores en el eje de abscisas y de ordenadas. Podríamos también, eso sí, hacer una representación de tres de esas ocho variables en un gráfico tridimensional. Pero aquí se acaba. Ya no podríamos visualizar una representación en más dimensiones. Por lo tanto, es imposible ver en un gráfico una representación de los 15 individuos respecto a todas las variables al mismo tiempo.
4. El ACP tiene como objetivo básico inicial suplir este déficit. Pretende, cuando vale la pena hacerlo (ya veremos cuándo vale la pena y cuándo no), realizar una representación de una nube de puntos multidimensional (de más de tres dimensiones), en dos o tres dimensiones. En definitiva, se trata de visualizar lo que no vemos. En nuestro ejemplo de los estudiantes de bachillerato el ACP trataría de hacer una representación de los 15 alumnos en dos o tres dimensiones pero contemplando todas las variables, sin prescindir de ninguna de ellas en el análisis.
5. Hay que hacer notar que, aunque el objetivo inicial es éste: la representación en dos o tres dimensiones de unos puntos que originariamente están en muchas dimensiones; o sea, visualizar lo que no vemos, la propia técnica, como consecuencia de su propio procedimiento, consigue crear unos objetos matemáticos (las componentes) muy interesantes que, en realidad, también podrían considerarse objetivos de la técnica porque, en muchas ocasiones, nos permiten establecer relaciones entre las variables, ver cómo se asocian, cómo se distancian, etc. De esto, no obstante, hablaré más tarde.
6. Vamos a ver el problema que estoy planteando pero miniaturizado. Así se entenderá mejor la esencia de la técnica. Supongamos que tenemos la siguiente representación bidimensional con dos variables X1 y X2:
7. Y supongamos que unos seres unidimensionales, que únicamente ven las cosas si están en una dimensión, quieren representar, en una única dimensión, esta nube de puntos que ellos, evidentemente, no pueden ver. Observemos que si lo que quieren es no prescindir de ninguna de las dos variables lo que pueden hacer es representar las proyecciones de los puntos sobre un eje como el dibujado en la siguiente figura:
8. Observemos que la nube de puntos roja, que está integrada por las proyecciones de los puntos originales sobre el nuevo eje, se parece bastante a la nube de puntos original. Las posiciones relativas de los puntos se respetan bastante. Y ahora los seres que sólo ven en una dimensión lo ven. Están viendo una representación unidimensional de una realidad bidimensional y lo hacen con bastante fidelidad. La nube de puntos roja se parece bastante a la negra. Ellos sólo ven la roja pero realmente es una buena aproximación de la original, que es la negra.
9. La representación en menos dimensiones no siempre tiene la misma calidad. En el gráfico siguiente vemos que a la izquierda la nube de puntos proyectada sobre el nuevo eje (la nube de puntos roja) se parece más a la original de lo que se parecen la roja y la negra en la situación mostrada en el gráfico de la derecha. Por lo tanto, en los datos de la derecha tiene menos valor realizar un ACP:
10. Y observemos que cuando he dibujado el eje para proyectar los valores sobre él lo he hecho situándolo de una forma, pero lo hubiera podido situar de otra. Observemos en el gráfico siguiente que el eje dispuesto en el ejemplo de la derecha no consigue, mediante la proyección de los puntos sobre ella, una nube de puntos representativa de la nube de puntos original:
11. Lo que hemos hecho es, en definitiva, un giro de los ejes de coordenadas sin tocar los puntos. Observemos lo que hemos hecho:
12. Lo importante es que ahora vemos la nube de puntos desde unos ejes donde uno es mucho más importante que el otro. Ahora los ejes son Y1 y Y2. Si X1 y X2 eran dos variables que tenían la misma cantidad de información, ahora Y1 y Y2 no tienen la misma cantidad de información. Y1 tiene mucha más información que Y2. En Estadística información es equivalente a dispersión, a varianza. Una variable que no varía no tiene información. Una variable que varía mucho tener el valor de un individuo es muy informativo.
13. El objetivo de la técnica ACP es, pues, éste: conseguir girar los ejes de tal forma que exista la mayor desigualdad posible entre la varianza de la nube de puntos original en las proyecciones en cada uno de los respectivos nuevos ejes y que, además, estos ejes, estas nuevas variables, sean independientes entre sí; o sea, que tengan correlación cero.
14. La búsqueda de estos nuevos ejes se hace mediante el cálculo de los llamados valores propios y vectores propios de la matriz de correlaciones entre todas las variables del estudio. Puede hacerse también a partir de otra matriz, la de varianzas-covarianzas, pero ésta tiene el problema de que cuando las variables tienen unidades de escala muy diferentes introduce un exceso de influencia por parte de las variables con mayor varianza. Por esto suele trabajarse con la matriz de correlaciones. De esta forma se unifica el peso de las variables iniciales del estudio. Suele hablarse de variables estandarizadas cuando se trabaja con la matriz de correlaciones. Una variable es estandarizada cuando la muestra se transforma a media cero y Desviación estándar uno. Esto se hace restando a cada valor muestral la media muestral y dividiendo por la Desviación estándar. De esta forma todas las variables del estudio tienen la misma media y la misma Desviación estándar y ninguna pesa más que otra. De esta forma la vocalización del estudio se pone en cómo es la forma de la nube de puntos, de cuáles son las relaciones entre las variables que permiten reducir dimensiones perdiendo el mínimo de información.
15. Algo muy importante: ¿Cuál es la relación existente entre las variables originales y las nuevas variables, los nuevos ejes; o sea, cuál es la relación, en el caso que hemos dibujado entre las variables X1 y X2 y las variables Y1 y Y2?
16. En primer lugar decir que a las variables Y1 y Y2, que son, eso, variables, también, como las originales, las llamamos en esta técnica “Componentes”. Y son cada una de ellas una combinación de las variables originales. Observemos la fórmula de esa combinación:
17. En realidad estos coeficientes que multiplican a las variables originales son los vectores propios de la matriz de correlaciones, es la fórmula de la transformación lineal realizada. Hemos cambiado de ejes y para llegar de los ejes originales a los nuevos ejes hace falta esta transformación. En definitiva, si tenemos un punto representado por las coordenadas originales, éstas son las fórmulas necesarias para conseguir las coordenadas de la nueva representación: la representación mediante los ejes constituidos por las componentes.
18. Si en el lugar de estar trabajando con dos variables originales estuviéramos trabajando con d variables originales la fórmula de las d componentes sería:
19. Se llama a la técnica Análisis de componentes principales porque transforma a las variables originales en nuevas variables, las componentes, las cuales tiene desigualdad en cuanto a la información explicada, lo que significa que tenemos unas componentes muy informativas y otras que no. Por eso tenemos unas componentes principales, que son las que usaremos para hacer la representación. Esta desigualdad generada al crear las componentes nos permite elegir, entre ellas, las principales y eliminar las poco importantes, cosa que no sucedía con las originales porque ellas eran todas principales, todas eran importantes, no podíamos prescindir de ninguna de ellas.
20. A los datos de los 15 estudiantes que se les ha evaluado en las ocho materias citadas en la matriz de datos mostrada al principio de este tema si se les hace un ACP tenemos la siguiente representación usando las dos primeras componentes principales: PCOMP_1 y PCOMP_2:
21. Observemos ahora que esta representación se asemeja mucho a la original en ocho dimensiones. Si observamos en el gráfico de dos dimensiones el alumno 1 y el 9 están muy próximos, prácticamente solapados. Miremos qué sucede en la matriz de datos. Observaremos que las notas, excepto Educación física, son prácticamente las mismas. Lo de Educación física tiene una explicación que ahora veremos.
22. Si, por el contrario, elegimos los individuos 5 y 12 vemos que en nuestro gráfico de dos dimensiones están completamente en los extremos, están en dos vértices de la representación. Si ahora miramos la matriz de datos veremos que el alumno 5 lo aprueba todo con buenas notas excepto la Educación física. En cambio el alumno 12 lo suspende todo, incluso la Educación física. Sorprendentemente en este caso son en todo distintos excepto en la Educación física que tienen justo la misma nota.
23. Por lo tanto, con el gráfico de dos dimensiones estamos viendo una muy buena fotografía de las posiciones relativas de los puntos en la representación de ocho dimensiones original que no vemos. Digo fotografía porque la metáfora es apropiada. Pensemos que cuando estamos viendo una fotografía en realidad estamos viendo una representación bidimensional de una realidad tridimensional. En el ACP estamos haciendo algo similar. Miramos de hacer una fotografía bidimensional o tridimensional, para que la podamos visualizar, de una realidad constituida por muchas dimensiones y que no visualizamos. Por lo tanto, en nuestro caso estamos viendo una fotografía bidimensional de una realidad ochodimensional.
24. Pero, algo muy importante: ¿Qué cantidad de información perdemos? Y, ¿qué representan los nuevos ejes?
25. Respecto a la cantidad de información observemos la siguiente tabla:
26. Los valores propios de cada componentes nos indican la cantidad de varianza, la cantidad de información que tiene cada componente. Como podemos ver en esta tabla la primera componente tiene un 46.38% de información y la segunda un 35.76%. Las dos juntas tienen un 82.14. Por lo tanto, haciendo una representación en dos dimensiones con esas dos primeras componentes perdemos un 17.86% de información únicamente.
27. Respecto a lo que representan los nuevos ejes observemos la fórmula de las dos primeras componentes principales:
28. Esto indica que la primera componente principal tiene los coeficientes de la primera columna y la segunda componente tiene los coeficientes de la segunda. O sea, que para conocer las coordenadas que tendrá cada alumno de esas dos componentes hay que multiplicar sus ocho notas por sus coeficientes respectivos. Y así es como obtenemos la representación gráfica bidimensional mostrada antes.
29. Para interpretar una componente hay que seguir el siguiente procedimiento: 1) Mirar el valor absoluto de los coeficientes distinguiendo los que tienen un valor grande y un valor pequeño. En nuestro caso en la primera componente observemos que Lengua, Inglés, Filosofía e Historia tienen coeficientes con valor absoluto grande, cercano en todos los casos a 0.5. Los demás ya son bastante más pequeños, pesan mucho menos en esta componente. En la segunda componente el peso principal se lo llevan Matemáticas, Física y Química, con coeficientes cercanos a 0.57. Las demás asignaturas pesan poco. 2) Mirar entre los coeficientes con valor absoluto grande el juego de signos que hay. En nuestro caso el signo es el mismo, por lo tanto, las variables que pesan en una componente y en la otra todas van en la misma dirección. Pero en otro caso nos podríamos encontrar con valores de signo contrario. Entonces hay que interpretar el juego de fuerzas de los signos.
30. En el ejemplo que venimos usando la interpretación es muy clara. En la primera componente tenemos reunidas las materias de letras. En la segunda componente tenemos reunidas, por el contrario, las materias de ciencias. La educación física no pesa ni en una ni en otra. Porque no tiene ninguna relación ni con las materias de letras ni con las de ciencias.
31. Viendo el gráfico bidimensional donde en el eje de las abscisas tenemos la primera componente y en el eje de las ordenadas tenemos la segunda componente podemos ver que los alumnos buenos en ciencias y letras estarán situados a la derecha y arriba, los alumnos buenos en letras y malos en ciencias se situarán a la derecha y abajo, los buenos en ciencias y malos en letras a la izquierda y arriba y, finalmente, los malos en ciencias y letras se situarán a la izquierda y abajo.
32. Veamos otro ejemplo de ACP. La matriz de datos son variables meteorológicas según comarcas catalanas el año 2005. Los datos son los siguientes:
33. Al hacer un ACP, los valores propios de las componentes principales son los siguientes:
34. Como puede verse con las dos primeras componentes explicamos el 77.41% de la varianza, de la información contenida en la nube de puntos original.
35. Y los vectores propios; o sea, los coeficientes de las dos primeras componentes, son los siguientes valores:
36. En la primera componente pesan; o sea, tiene valor absoluto grande, las tres variables de temperatura y la altitud media de la comarca. Además lo hacen las temperaturas con signo positivo y la altitud con signo negativo. Lo que indica que valores grandes de la primera componente corresponden a comarcas con temperaturas altas y altitud baja. Altitud baja porque como el coeficiente es negativo para que la componente tenga un valor alto hace falta que la altitud reste poco, sea un valor pequeño. Contrariamente, valores pequeños de esta primera componente indica temperaturas bajas y altitud alta.
37. En la segunda componente pesan especialmente las variables Precipitaciones, Humedad y Velocidad del viento. Las dos primeras con signo positivo y la tercera con signo negativo. Valores grandes de esta componente indicarán zonas con mucha lluvia, mucha humedad y poco viento. Por el contrario, valores bajos de esta segunda componente corresponderán a comarcas de bajas precipitaciones, baja humedad y alta velocidad del viento.
38. La representación de las comarcas según las dos primeras componentes es la siguiente:
39. Viendo el gráfico y la anterior interpretación de las componentes podemos dividir el gráfico en cuatro cuadrantes y afirmar: 1) Arriba a la derecha: Comarcas calurosas y húmedas. 2) Abajo a la derecha: Comarcas calurosas y secas. 3) Arriba a la izquierda: Comarcas frías y húmedas. 4) Abajo a la izquierda: Comarcas frías y secas.
40. Observemos, pues, que conseguimos con esta técnica representar en pocas dimensiones una realidad multidimensional y, también, crear estas componentes, estas variables de variables, variables que son combinación de las variables originales. Y estas combinaciones son interesantes en sí mismas, porque nos ayudan a crear una especie de conglomerados de variables combinadas de una forma que, en realidad, reflejan la vida interna que tienen ellas entre sí en cuanto a la covariación conjunta.
41. En el primer ejemplo, el caso de las notas, las componentes nos han creado la noción de Letras y la noción de Ciencias, reflejando una idea que todos tenemos en mente: que las capacidades hacia un ámbito u otro son como dos dimensiones independientes que se pueden tener ambas, que se puede tener una y no otra o que se puede, también, no tener ninguna.
42. En el segundo ejemplo, las componentes nos separan dos elementos independientes: aspectos de frío o calor, ligados a la altitud de la zona, por un lado, y aspectos referentes a la humedad climática, por otro. Aspectos que pueden ir asociados entre sí de forma independiente creando cuatro tipos de comarcas o de zonas distintas según la combinación de los valores extremos de estas dos componentes.
43. Otro ejemplo de Análisis de componentes aplicado a datos de jugadores de baloncesto se puede consultar en el fichero Análisis de componentes principales aplicado a datos de jugadores de baloncesto.
44. Otro ejemplo interesante es el planteado en la Situación 66, donde aparecen unos datos de diferentes países y las proporciones que tienen que hay en ellos en cuanto a las distintas formaciones universitarias. El análisis de los datos los podéis ver en la Solución Situación 66.
45. Otro ejemplo, ahora con Pokémons, está planteado en la Situación 47. La solución se puede ver en el fichero Solución Situación 47.
46. Un ejemplo de fútbol lo tenemos en la Situación 46. La solución puede verse en el fichero Solución Situación 46.
47. Como puede verse, en este tema hemos hablado de una técnica esencialmente descriptiva. No hemos hablado, aquí, de otra cosa que de muestras. No hay voluntad inferencial en esta técnica. Es cierto que se ha estudiado y creado técnicas inferenciales relacionadas con el ACP pero no es muy utilizada en la práctica. Es por ello que debemos considerarla una técnica descriptiva, una técnica que intenta buscar la representación de una muestra de individuos de los que tenemos muchas variables de interés. Una técnica donde la muestra es la finalidad.
48. Podéis practicar los conceptos de este tema con ejercicios comentados en el siguiente:






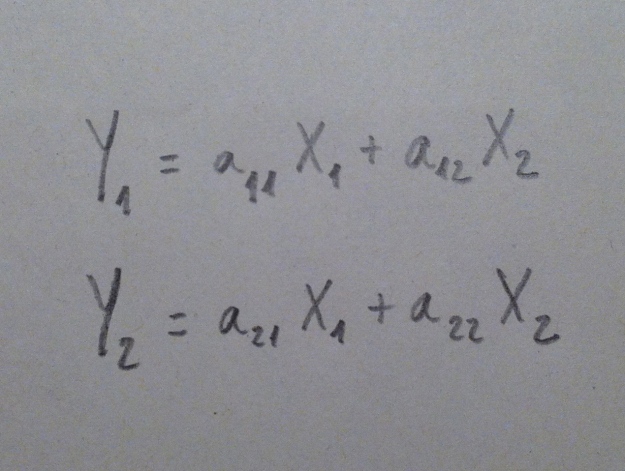
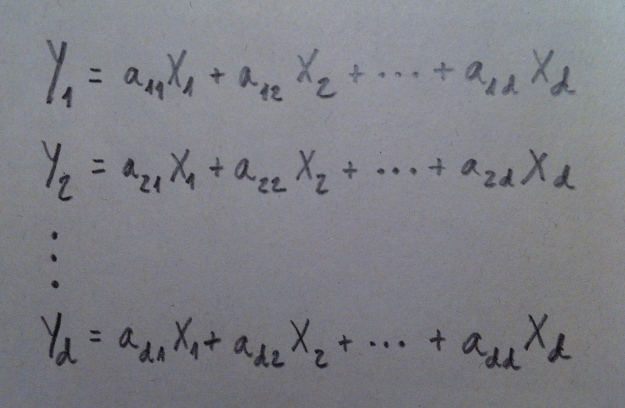







Enhorabuena por el blog, me ha quedado más claro el ACP con sus explicaciones que mirando todos los vídeos de youtube. Me gustaría hacerle dos preguntas,
¿se pueden introducir variables categóricas en un ACP? y la otra, ¿puede servir para analizar escalas likert?
Un saludo y muchas gracias por las explicaciones!
Se pueden entrar variables cualitativas que tengan polaridad, que puedan etiquetarse numéricamente con una numeración con sentido. Las variables likert son un ejemplo de ello. Se pueden usar claramente en ACP